KMP

Kmp算法是一种查询字符串匹配的算法。

比如说，有一个字符串”ABC CCACAC BACCACB”，想知道里面是否包含了另一个字符串”CCACB”？

ABC CCACCA BACCACB

​ CCACB

1.

先对对比两个字符串的第一个字母。第一个字母，A，C是不匹配的。所以继续向后移动一位。

2.

位移一位以后发现B,C也是不匹配的。所以再位移到和查找的字符串第一个字母匹配的地方。

3.

位移到与查找字符串第一个字母匹配的地方。接着再位移依次比较。

4.

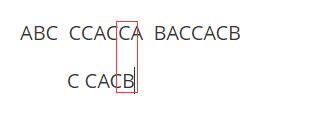
直到出现有一个字母和搜索的字符不相同。

5.

这个时候，最容易想到的是，将整个查找词整个后移动一位，再从头比较，这样是可行的，但是效率过低。因为要把搜索查找过的词语再查找一次。

6.

当比较到C，B不匹配的时候，其是知道前面的“CCAC”是匹配的，KMP算法的想法就是，利用这个已知信息，不把搜索的位置移动回到已经比较过的位置，这样就提高了效率。

这里就引入一个部分匹配的表：

首先，了解两个概念：

“前缀”：指除了最后一个字符串以外，一个字符串的全部头部组合。

”后缀“：指除了第一个字符以外，一个字符串的全部尾部组合。

以“CCACB”为例子：

- “C”的前缀和后缀都是空集，共有的元素是0
- “CC”的前缀是[C]，后缀是[C],共有元素是1
- “CCA”的前缀是[C,CC]，后缀是[C,CA],共元素是1
- “CCAC”的前缀是[C,CC,CCA],后缀是[C,CA,CAC],共有元素是1
- “CCACB”的前缀是[C,CC,CCA,CCAC],后缀是[C,CA,CAC,CACB],共有元素是1

这样的得到部分匹配表：

搜索词	C	C	A	C	B
部分匹配值	0	1	1	1	1

7.

在比较到C，B不匹配的时候。查询匹配表，可知最后一个匹配的字符“C”对应的部分匹配值是1。按照下面的公式计算出移动的位数：

​

移动位数 = 已匹配的字符数 - 对挺的部分匹配值

所以移动的位数是 4 - 1 = 3。

8.

这样一直匹配就可以得到是否包含了这个字符串。